2019-11-02 12:07:41 +08:00
|
|
|
# 10.2 矩形覆盖
|
|
|
|
|
|
2019-11-03 23:57:08 +08:00
|
|
|
## 题目链接
|
|
|
|
|
|
2022-01-07 09:00:01 +00:00
|
|
|
[牛客网](https://www.nowcoder.com/practice/72a5a919508a4251859fb2cfb987a0e6?tpId=13\&tqId=11163\&tPage=1\&rp=1\&ru=/ta/coding-interviews\&qru=/ta/coding-interviews/question-ranking\&from=cyc\_github)
|
2019-11-02 12:07:41 +08:00
|
|
|
|
|
|
|
|
## 题目描述
|
|
|
|
|
|
|
|
|
|
我们可以用 2\*1 的小矩形横着或者竖着去覆盖更大的矩形。请问用 n 个 2\*1 的小矩形无重叠地覆盖一个 2\*n 的大矩形,总共有多少种方法?
|
|
|
|
|
|
2022-01-07 09:00:01 +00:00
|
|
|
\
|
|
|
|
|
|
2019-11-02 12:07:41 +08:00
|
|
|
|
|
|
|
|
## 解题思路
|
|
|
|
|
|
|
|
|
|
当 n 为 1 时,只有一种覆盖方法:
|
|
|
|
|
|
2022-01-07 09:00:01 +00:00
|
|
|
\
|
|
|
|
|
|
2019-11-02 12:07:41 +08:00
|
|
|
|
|
|
|
|
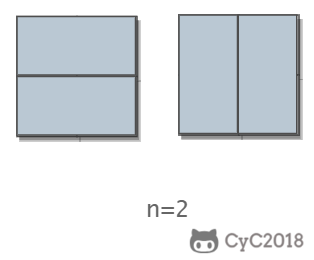
当 n 为 2 时,有两种覆盖方法:
|
|
|
|
|
|
2022-01-07 09:00:01 +00:00
|
|
|
\
|
|
|
|
|
|
2019-11-02 12:07:41 +08:00
|
|
|
|
|
|
|
|
要覆盖 2\*n 的大矩形,可以先覆盖 2\*1 的矩形,再覆盖 2\*(n-1) 的矩形;或者先覆盖 2\*2 的矩形,再覆盖 2\*(n-2) 的矩形。而覆盖 2\*(n-1) 和 2\*(n-2) 的矩形可以看成子问题。该问题的递推公式如下:
|
|
|
|
|
|
2022-01-07 09:00:01 +00:00
|
|
|
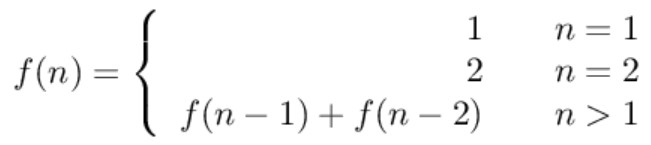\
|
2019-11-02 12:07:41 +08:00
|
|
|
|
|
|
|
|
|
|
|
|
|
```java
|
2021-03-23 02:48:19 +08:00
|
|
|
public int rectCover(int n) {
|
2019-11-02 12:07:41 +08:00
|
|
|
if (n <= 2)
|
|
|
|
|
return n;
|
|
|
|
|
int pre2 = 1, pre1 = 2;
|
|
|
|
|
int result = 0;
|
|
|
|
|
for (int i = 3; i <= n; i++) {
|
|
|
|
|
result = pre2 + pre1;
|
|
|
|
|
pre2 = pre1;
|
|
|
|
|
pre1 = result;
|
|
|
|
|
}
|
|
|
|
|
return result;
|
|
|
|
|
}
|
|
|
|
|
```
|