diff --git a/docs/notes/Leetcode 题解 - 双指针.md b/docs/notes/Leetcode 题解 - 双指针.md
index 7e0fdc8b..12451fe1 100644
--- a/docs/notes/Leetcode 题解 - 双指针.md	
+++ b/docs/notes/Leetcode 题解 - 双指针.md	
@@ -30,8 +30,7 @@ Output: index1=1, index2=2
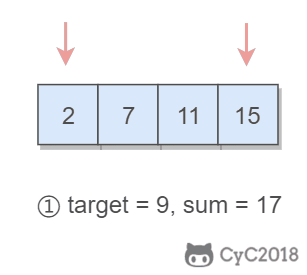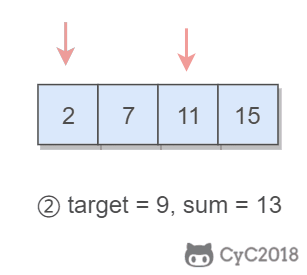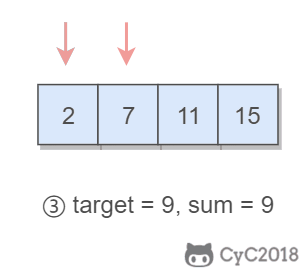
 - 如果 sum > target，移动较大的元素，使 sum 变小一些；
 - 如果 sum < target，移动较小的元素，使 sum 变大一些。
 
-数组中的元素最多遍历一次，时间复杂度为 O(N)。额外只使用了两个变量，空间复杂度为 
-O(1)。
+数组中的元素最多遍历一次，时间复杂度为 O(N)。只使用了两个额外变量，空间复杂度为  O(1)。
 
 <div align="center"> <img src="https://cs-notes-1256109796.cos.ap-guangzhou.myqcloud.com/437cb54c-5970-4ba9-b2ef-2541f7d6c81e.gif" width="200px"> </div><br>
 
@@ -65,23 +64,32 @@ Output: True
 Explanation: 1 * 1 + 2 * 2 = 5
 ```
 
-题目描述：判断一个数是否为两个数的平方和。
+题目描述：判断一个非负整数是否为两个整数的平方和。
+
+可以看成是在元素为 1\~target 的有序数组中查找两个数，使得这两个数的平方和为 target，如果能找到，则返回 true，表示 target 是两个整数的平方和。
+
+本题和 167\. Two Sum II - Input array is sorted 类似，只有一个明显区别：一个是求和为 target，一个是平方和为 target。可以和 167 一样使用双指针得到两个数，使其平方和为 target。
+
+这题的关键是右指针的初始化，实现剪枝，从而降低时间复杂度。设右指针为 x，左指针固定为 1，为了使 1<sup>2</sup> + x<sup>2</sup> 的值尽可能接近 target，我们可以将 x 取为 sqrt(target)。
+
+因为最多只需要遍历一次 1\~sqrt(target)，所以时间复杂度为 O(log<sub>2</sub>N)。又因为只使用了两个额外的变量，因此空间复杂度为 O(1)。
 
 ```java
-public boolean judgeSquareSum(int c) {
-    int i = 0, j = (int) Math.sqrt(c);
-    while (i <= j) {
-        int powSum = i * i + j * j;
-        if (powSum == c) {
-            return true;
-        } else if (powSum > c) {
-            j--;
-        } else {
-            i++;
-        }
-    }
-    return false;
-}
+ public boolean judgeSquareSum(int target) {
+     if (target <= 0) return false;
+     int i = 0, j = (int) Math.sqrt(target);
+     while (i <= j) {
+         int powSum = i * i + j * j;
+         if (powSum == target) {
+             return true;
+         } else if (powSum > target) {
+             j--;
+         } else {
+             i++;
+         }
+     }
+     return false;
+ }
 ```
 
 # 3. 反转字符串中的元音字符
diff --git a/notes/Leetcode 题解 - 双指针.md b/notes/Leetcode 题解 - 双指针.md
index c189d37c..54c11d81 100644
--- a/notes/Leetcode 题解 - 双指针.md	
+++ b/notes/Leetcode 题解 - 双指针.md	
@@ -30,8 +30,7 @@ Output: index1=1, index2=2
 - 如果 sum > target，移动较大的元素，使 sum 变小一些；
 - 如果 sum < target，移动较小的元素，使 sum 变大一些。
 
-数组中的元素最多遍历一次，时间复杂度为 O(N)。额外只使用了两个变量，空间复杂度为 
-O(1)。
+数组中的元素最多遍历一次，时间复杂度为 O(N)。只使用了两个额外变量，空间复杂度为  O(1)。
 
 <div align="center"> <img src="pics/437cb54c-5970-4ba9-b2ef-2541f7d6c81e.gif" width="200px"> </div><br>
 
@@ -65,23 +64,32 @@ Output: True
 Explanation: 1 * 1 + 2 * 2 = 5
 ```
 
-题目描述：判断一个数是否为两个数的平方和。
+题目描述：判断一个非负整数是否为两个整数的平方和。
+
+可以看成是在元素为 1\~target 的有序数组中查找两个数，使得这两个数的平方和为 target，如果能找到，则返回 true，表示 target 是两个整数的平方和。
+
+本题和 167\. Two Sum II - Input array is sorted 类似，只有一个明显区别：一个是求和为 target，一个是平方和为 target。可以和 167 一样使用双指针得到两个数，使其平方和为 target。
+
+这题的关键是右指针的初始化，实现剪枝，从而降低时间复杂度。设右指针为 x，左指针固定为 1，为了使 1<sup>2</sup> + x<sup>2</sup> 的值尽可能接近 target，我们可以将 x 取为 sqrt(target)。
+
+因为最多只需要遍历一次 1\~sqrt(target)，所以时间复杂度为 O(log<sub>2</sub>N)。又因为只使用了两个额外的变量，因此空间复杂度为 O(1)。
 
 ```java
-public boolean judgeSquareSum(int c) {
-    int i = 0, j = (int) Math.sqrt(c);
-    while (i <= j) {
-        int powSum = i * i + j * j;
-        if (powSum == c) {
-            return true;
-        } else if (powSum > c) {
-            j--;
-        } else {
-            i++;
-        }
-    }
-    return false;
-}
+ public boolean judgeSquareSum(int target) {
+     if (target <= 0) return false;
+     int i = 0, j = (int) Math.sqrt(target);
+     while (i <= j) {
+         int powSum = i * i + j * j;
+         if (powSum == target) {
+             return true;
+         } else if (powSum > target) {
+             j--;
+         } else {
+             i++;
+         }
+     }
+     return false;
+ }
 ```
 
 # 3. 反转字符串中的元音字符