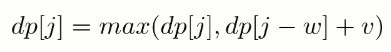diff --git a/docs/notes/Leetcode 题解 - 动态规划.md b/docs/notes/Leetcode 题解 - 动态规划.md
index 5c55c0bc..018fbee0 100644
--- a/docs/notes/Leetcode 题解 - 动态规划.md
+++ b/docs/notes/Leetcode 题解 - 动态规划.md
@@ -630,6 +630,10 @@ public int lengthOfLCS(int[] nums1, int[] nums2) {

```java
+// W 为背包总体积
+// N 为物品数量
+// weights 数组存储 N 个物品的重量
+// values 数组存储 N 个物品的价值
public int knapsack(int W, int N, int[] weights, int[] values) {
int[][] dp = new int[N + 1][W + 1];
for (int i = 1; i <= N; i++) {
@@ -654,7 +658,7 @@ public int knapsack(int W, int N, int[] weights, int[] values) {
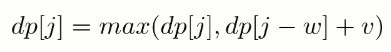
-因为 dp[j-w] 表示 dp[i-1][j-w],因此不能先求 dp[i][j-w],以防将 dp[i-1][j-w] 覆盖。也就是说要先计算 dp[i][j] 再计算 dp[i][j-w],在程序实现时需要按倒序来循环求解。
+因为 dp[j-w] 表示 dp[i-1][j-w],因此不能先求 dp[i][j-w],防止将 dp[i-1][j-w] 覆盖。也就是说要先计算 dp[i][j] 再计算 dp[i][j-w],在程序实现时需要按倒序来循环求解。
```java
public int knapsack(int W, int N, int[] weights, int[] values) {
@@ -861,7 +865,7 @@ return -1.
- 物品大小:面额
- 物品价值:数量
-因为硬币可以重复使用,因此这是一个完全背包问题。完全背包只需要将 0-1 背包中逆序遍历 dp 数组改为正序遍历即可。
+因为硬币可以重复使用,因此这是一个完全背包问题。完全背包只需要将 0-1 背包的逆序遍历 dp 数组改为正序遍历即可。
```java
public int coinChange(int[] coins, int amount) {
@@ -926,9 +930,15 @@ dict = ["leet", "code"].
Return true because "leetcode" can be segmented as "leet code".
```
-dict 中的单词没有使用次数的限制,因此这是一个完全背包问题。该问题涉及到字典中单词的使用顺序,因此可理解为涉及顺序的完全背包问题。
+dict 中的单词没有使用次数的限制,因此这是一个完全背包问题。
-求解顺序的完全背包问题时,对物品的迭代应该放在最里层。
+该问题涉及到字典中单词的使用顺序,也就是说物品必须按一定顺序放入背包中,例如下面的 dict 就不够组成字符串 "leetcode":
+
+```html
+["lee", "tc", "cod"]
+```
+
+求解顺序的完全背包问题时,对物品的迭代应该放在最里层,对背包的迭代放在外层,只有这样才能让物品按一定顺序放入背包中。
```java
public boolean wordBreak(String s, List wordDict) {
diff --git a/notes/Leetcode 题解 - 动态规划.md b/notes/Leetcode 题解 - 动态规划.md
index 915fdc44..047a11c1 100644
--- a/notes/Leetcode 题解 - 动态规划.md
+++ b/notes/Leetcode 题解 - 动态规划.md
@@ -630,6 +630,10 @@ public int lengthOfLCS(int[] nums1, int[] nums2) {
```java
+// W 为背包总体积
+// N 为物品数量
+// weights 数组存储 N 个物品的重量
+// values 数组存储 N 个物品的价值
public int knapsack(int W, int N, int[] weights, int[] values) {
int[][] dp = new int[N + 1][W + 1];
for (int i = 1; i <= N; i++) {
@@ -654,7 +658,7 @@ public int knapsack(int W, int N, int[] weights, int[] values) {
-因为 dp[j-w] 表示 dp[i-1][j-w],因此不能先求 dp[i][j-w],以防将 dp[i-1][j-w] 覆盖。也就是说要先计算 dp[i][j] 再计算 dp[i][j-w],在程序实现时需要按倒序来循环求解。
+因为 dp[j-w] 表示 dp[i-1][j-w],因此不能先求 dp[i][j-w],防止将 dp[i-1][j-w] 覆盖。也就是说要先计算 dp[i][j] 再计算 dp[i][j-w],在程序实现时需要按倒序来循环求解。
```java
public int knapsack(int W, int N, int[] weights, int[] values) {
@@ -861,7 +865,7 @@ return -1.
- 物品大小:面额
- 物品价值:数量
-因为硬币可以重复使用,因此这是一个完全背包问题。完全背包只需要将 0-1 背包中逆序遍历 dp 数组改为正序遍历即可。
+因为硬币可以重复使用,因此这是一个完全背包问题。完全背包只需要将 0-1 背包的逆序遍历 dp 数组改为正序遍历即可。
```java
public int coinChange(int[] coins, int amount) {
@@ -926,9 +930,15 @@ dict = ["leet", "code"].
Return true because "leetcode" can be segmented as "leet code".
```
-dict 中的单词没有使用次数的限制,因此这是一个完全背包问题。该问题涉及到字典中单词的使用顺序,因此可理解为涉及顺序的完全背包问题。
+dict 中的单词没有使用次数的限制,因此这是一个完全背包问题。
-求解顺序的完全背包问题时,对物品的迭代应该放在最里层。
+该问题涉及到字典中单词的使用顺序,也就是说物品必须按一定顺序放入背包中,例如下面的 dict 就不够组成字符串 "leetcode":
+
+```html
+["lee", "tc", "cod"]
+```
+
+求解顺序的完全背包问题时,对物品的迭代应该放在最里层,对背包的迭代放在外层,只有这样才能让物品按一定顺序放入背包中。
```java
public boolean wordBreak(String s, List wordDict) {