数据结构

interview/struct/datastruct.md

@@ -8,6 +8,12 @@
         - [完全二叉树](#完全二叉树)
         - [二叉查找树](#二叉查找树)
     - [AVL树](#avl树)
+    - [RBT 红黑树](#rbt-红黑树)
+    - [B-树](#b-树)
+    - [B+树](#b树)
+    - [B*树](#b树)
+    - [B B- B+ B* 树总结](#b-b--b-b-树总结)
+    - [B+/B*Tree应用](#bbtree应用)
 - [参考链接](#参考链接)
 
 <!-- /TOC -->
@@ -75,7 +81,158 @@
 
 ## AVL树
 
-定义：自平衡二叉查找树
+定义：自平衡二叉查找树,平衡二叉树或为空树,或为如下性质的二叉排序树:
+
+（1）左右子树深度之差的绝对值不超过1;
+（2）左右子树仍然为平衡二叉树.
+平衡因子BF=左子树深度－右子树深度.
+
+平衡二叉树每个结点的平衡因子只能是1，0，-1。若其绝对值超过1，则该二叉排序树就是不平衡的。
+
+## RBT 红黑树
+
+AVL是严格平衡树，因此在增加或者删除节点的时候，根据不同情况，旋转的次数比红黑树要多；
+红黑是**弱平衡**的，用非严格的平衡来换取增删节点时候旋转次数的降低；
+
+所以简单说，**搜索的次数远远大于插入和删除，那么选择AVL树，如果搜索，插入删除次数几乎差不多，应该选择RB树。**
+
+红黑树上每个结点内含五个域，color，key，left，right，p。如果相应的指针域没有，则设为NIL。
+一般的，红黑树，满足以下性质，即只有满足以下全部性质的树，我们才称之为红黑树：
+1）每个结点要么是红的，要么是黑的。
+2）根结点是黑的。
+3）每个叶结点，即空结点（NIL）是黑的。
+4）如果一个结点是红的，那么它的俩个儿子都是黑的。
+5）对每个结点，从该结点到其子孙结点的所有路径上包含相同数目的黑结点。
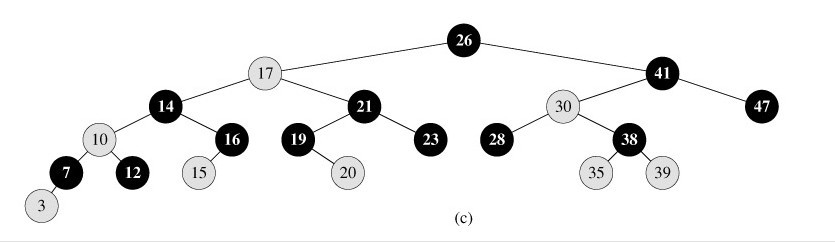
+下图所示，即是一颗红黑树：
+
+![](http://hi.csdn.net/attachment/201012/29/8394323_1293613306CGzE.jpg)
+
+## B-树
+
+定义：B树是一种平衡多路搜索树（并不是二叉的），满足如下性质：
+
+1.定义任意非叶子结点最多只有M个儿子；且M>2；
+
+2.根结点的儿子数为[2, M]；
+
+3.除根结点以外的非叶子结点的儿子数为[M/2, M]；
+
+4.每个结点存放至少M/2-1（取上整）和至多M-1个关键字；（至少2个关键字）
+
+5.非叶子结点的关键字个数=指向儿子的指针个数-1；
+
+6.非叶子结点的关键字：K[1], K[2], …, K[M-1]；且K[i] < K[i+1]；
+
+7.非叶子结点的指针：P[1], P[2], …, P[M]；其中P[1]指向关键字小于K[1]的
+
+子树，P[M]指向关键字大于K[M-1]的子树，其它P[i]指向关键字属于(K[i-1], K[i])的子树；
+
+8.所有叶子结点位于同一层；
+
+如M=3:
+
+![](img/4.jpg)
+
+B-树的搜索，从根结点开始，对结点内的关键字（有序）序列进行二分查找，如果
+
+命中则结束，否则进入查询关键字所属范围的儿子结点；重复，直到所对应的儿子指针为
+
+空，或已经是叶子结点；
+
+B-树的特性：
+
+1.关键字集合分布在整颗树中；
+
+2.任何一个关键字出现且只出现在一个结点中；
+
+3.搜索有可能在非叶子结点结束；
+
+4.其搜索性能等价于在关键字全集内做一次二分查找；
+
+5.自动层次控制；
+
+由于限制了除根结点以外的非叶子结点，至少含有M/2个儿子，确保了结点的至少
+
+利用率，其最底搜索性能为：
+
+![](img/0.JPG)
+
+其中，M为设定的非叶子结点最多子树个数，N为关键字总数；
+
+所以B-树的性能总是等价于二分查找（与M值无关），也就没有B树平衡的问题；
+
+由于M/2的限制，在插入结点时，如果结点已满，需要将结点分裂为两个各占
+
+M/2的结点；删除结点时，需将两个不足M/2的兄弟结点合并；
+
+## B+树
+
+定义：B+树是B-树的变体，也是一种多路搜索树：
+
+1.其定义基本与B-树同，除了：
+
+2.非叶子结点的子树指针与关键字个数相同；
+
+3.非叶子结点的子树指针P[i]，指向关键字值属于[K[i], K[i+1])的子树
+
+（B-树是开区间）；
+
+5.为所有叶子结点增加一个链指针；
+
+6.所有关键字都在叶子结点出现；
+
+如：（M=3）
+
+![](img/5.JPG)
+
+B+的搜索与B-树也基本相同，区别是B+树只有达到叶子结点才命中（B-树可以在
+非叶子结点命中），其性能也等价于在关键字全集做一次二分查找；
+
+B+的特性：
+
+1.所有关键字都出现在叶子结点的链表中（稠密索引），且链表中的关键字恰好是有序的；
+
+2.不可能在非叶子结点命中；
+
+3.非叶子结点相当于是叶子结点的索引（稀疏索引），叶子结点相当于是存储（关键字）数据的数据层；
+
+4.更适合文件索引系统；比如对已经建立索引的数据库记录，查找10<=id<=20，那么只要通过根节点搜索到id=10的叶节点，之后只要根据叶节点的链表找到第一个大于20的就行了，比B-树在查找10到20内的每一个时每次都从根节点出发查找提高了不少效率。
+
+## B*树
+
+定义：B*树是B+树的变体，在B+树的非根和非叶子结点再增加指向兄弟的指针；
+
+![](img/6.JPG)
+
+B\*树定义了非叶子结点关键字个数至少为(2/3)\*M，即块的最低使用率为2/3（代替B+树的1/2）；
+
+B+树的分裂：当一个结点满时，分配一个新的结点，并将原结点中1/2的数据复制到新结点，最后在父结点中增加新结点的指针；B+树的分裂只影响原结点和父结点，而不会影响兄弟结点，所以它不需要指向兄弟的指针；
+
+B*树的分裂：当一个结点满时，如果它的下一个兄弟结点未满，那么将一部分数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字（因为兄弟结点的关键字范围改变了）；如果兄弟也满了，则在原结点与兄弟结点之间增加新结点，并各复制1/3的数据到新结点，最后在父结点增加新结点的指针；
+
+**所以，B*树分配新结点的概率比B+树要低，空间使用率更高；**
+
+## B B- B+ B* 树总结
+
+B树：二叉树，每个结点只存储一个关键字，等于则命中，小于走左结点，大于走右结点；
+
+B-树：多路搜索树，每个结点存储M/2到M个关键字，非叶子结点存储指向关键字范围的子结点；所有关键字在整颗树中出现，且只出现一次，非叶子结点可以命中；
+
+B+树：在B-树基础上，为叶子结点增加链表指针，所有关键字都在叶子结点中出现，非叶子结点作为叶子结点的索引；B+树总是到叶子结点才命中；
+
+B*树：在B+树基础上，为非叶子结点也增加链表指针，将结点的最低利用率从1/2提高到2/3；
+
+## B+/B*Tree应用
+
+数据库索引--索引文件和数据文件是分离的，索引文件仅保存数据记录的地址。
+
+
+数据库索引--表数据文件本身就是按B+Tree组织的一个索引结构，这棵树的叶节点data域保存了完整的数据记录。这个索引的key是数据表的主键。
+
+
+倒排索引--也可以由B树及其变种实现但不一定非要B树及其变种实现，如lucene没有使用B树结构，因此lucene可以用二分搜索算法快速定位关键词。实现时，lucene将下面三列分别作为词典文件（Term Dictionary）、频率文件(frequencies)、位置文件 (positions)保存。其中词典文件不仅保存有每个关键词，还保留了指向频率文件和位置文件的指针，通过指针可以找到该关键字的频率信息和位置信息。 　　
+
+参考链接：[B-树和B+树的应用：数据搜索和数据库索引](http://blog.csdn.net/hguisu/article/details/7786014)
 
 # 参考链接