83 lines
3.7 KiB
Markdown
83 lines
3.7 KiB
Markdown
<!-- TOC -->
|
||
|
||
- [树](#树)
|
||
- [二叉树](#二叉树)
|
||
- [二叉树定义](#二叉树定义)
|
||
- [二叉树性质](#二叉树性质)
|
||
- [满二叉树](#满二叉树)
|
||
- [完全二叉树](#完全二叉树)
|
||
- [二叉查找树](#二叉查找树)
|
||
- [AVL树](#avl树)
|
||
- [参考链接](#参考链接)
|
||
|
||
<!-- /TOC -->
|
||
|
||
# 树
|
||
|
||
1. 树的定义
|
||
|
||
树是一种数据结构,它是由n(n>=1)个有限节点组成一个具有层次关系的集合。
|
||
|
||
2. 基本术语
|
||
|
||
若一个结点有子树,那么该结点称为子树根的"双亲",子树的根是该结点的"孩子"。有相同双亲的结点互为"兄弟"。一个结点的所有子树上的任何结点都是该结点的后裔。从根结点到某个结点的路径上的所有结点都是该结点的祖先。
|
||
|
||
结点的度:结点拥有的子树的数目。
|
||
叶子:度为零的结点。
|
||
分支结点:度不为零的结点。
|
||
树的度:树中结点的最大的度。
|
||
|
||
层次:根结点的层次为1,其余结点的层次等于该结点的双亲结点的层次加1。
|
||
树的高度:树中结点的最大层次。
|
||
无序树:如果树中结点的各子树之间的次序是不重要的,可以交换位置。
|
||
有序树:如果树中结点的各子树之间的次序是重要的, 不可以交换位置。
|
||
森林:0个或多个不相交的树组成。对森林加上一个根,森林即成为树;删去根,树即成为森林。
|
||
|
||
## 二叉树
|
||
|
||
### 二叉树定义
|
||
|
||
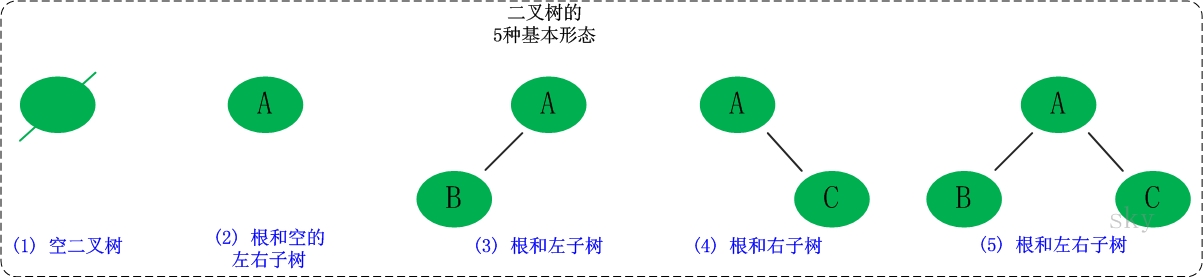
二叉树是每个节点最多有两个子树的树结构。它有五种基本形态:二叉树可以是空集;根可以有空的左子树或右子树;或者左、右子树皆为空。
|
||
|
||
|
||
|
||
### 二叉树性质
|
||
|
||
性质1:二叉树第i层上的结点数目最多为 2^(k-1) (i≥1)。
|
||
性质2:深度为k的二叉树至多有2^k - 1个结点(k≥1)。
|
||
性质3:包含n个结点的二叉树的高度至少为log2 (n+1)。
|
||
性质4:在任意一棵二叉树中,若终端结点的个数为n0,度为2的结点数为n2,则n0=n2+1。
|
||
|
||
### 满二叉树
|
||
|
||
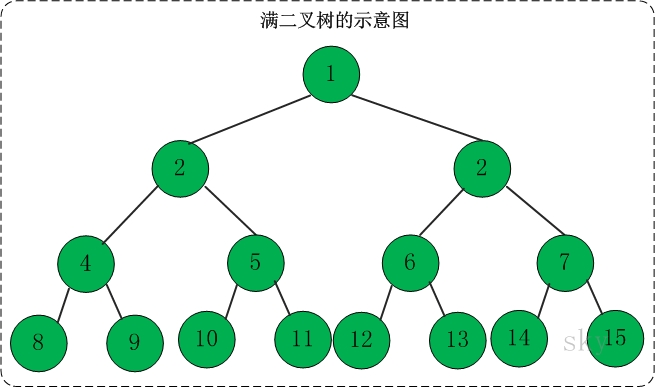
定义:高度为h,并且由2{h} –1个结点的二叉树,被称为满二叉树。
|
||
|
||
|
||
|
||
### 完全二叉树
|
||
|
||
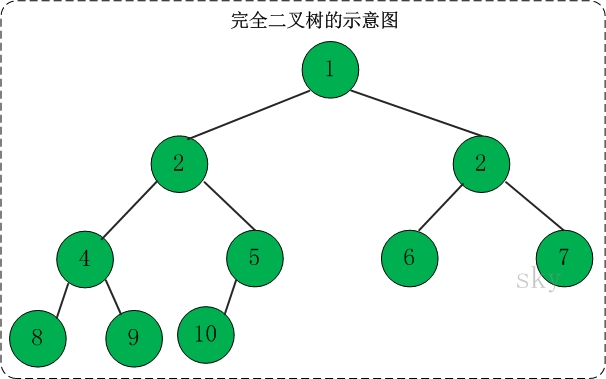
定义:一棵二叉树中,只有最下面两层结点的度可以小于2,并且最下一层的叶结点集中在靠左的若干位置上。这样的二叉树称为完全二叉树。
|
||
特点:叶子结点只能出现在最下层和次下层,且最下层的叶子结点集中在树的左部。显然,一棵满二叉树必定是一棵完全二叉树,而完全二叉树未必是满二叉树。
|
||
|
||
|
||
|
||
### 二叉查找树
|
||
|
||
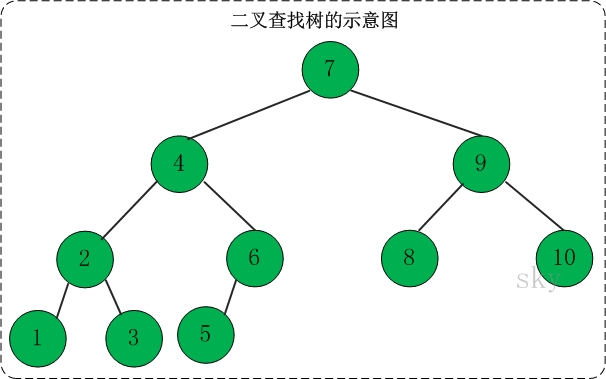
定义:二叉查找树(Binary Search Tree),又被称为**二叉搜索树**。设x为二叉查找树中的一个结点,x节点包含关键字key,节点x的key值记为key[x]。如果y是x的左子树中的一个结点,则key[y] <= key[x];如果y是x的右子树的一个结点,则key[y] >= key[x]。
|
||
|
||
|
||
|
||
在二叉查找树中:
|
||
(01) 若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
|
||
(02) 任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
|
||
(03) 任意节点的左、右子树也分别为二叉查找树。
|
||
(04) **没有键值相等的节点(no duplicate nodes)。**
|
||
|
||
## AVL树
|
||
|
||
定义:自平衡二叉查找树
|
||
|
||
# 参考链接
|
||
|
||
- [数据结构](https://blog.csdn.net/qq_31196849/article/details/78529724)
|
||
- [数据结构全](https://blog.csdn.net/heyuchang666/article/details/49891635) |